Laws of hydrodynamics

Moving efficiently underwater with a monofin in order to achieve a performance requires an understanding of the monofin swimming technique. To fully understand this technique, you need to have an idea of the laws of hydrodynamics. These laws allow you to understand the environment in which you are moving and help to establish technical principles.

When you move through water, you will encounter and create resistance. These resistances tend to slow down your movement.

Forward resistance

Two important concepts are those of frontal surface and form coefficient :

Frontal Area : it is the cross-section of the body moving through the water, which is exposed to the resistance of the water.

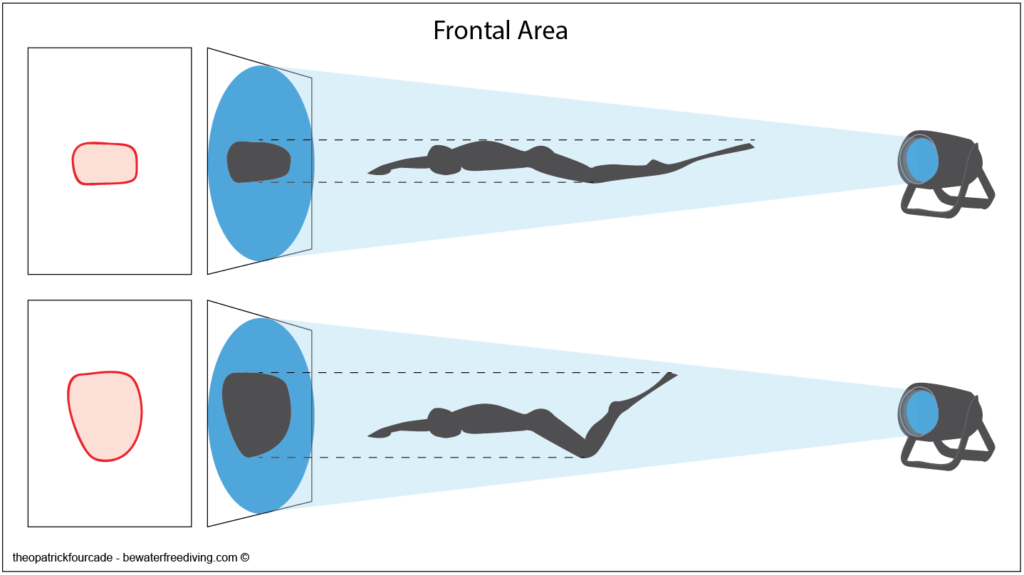
The ‘Shape Coefficient’: This is the total shape of the body. The same master couple can be presented with a different total shape. 

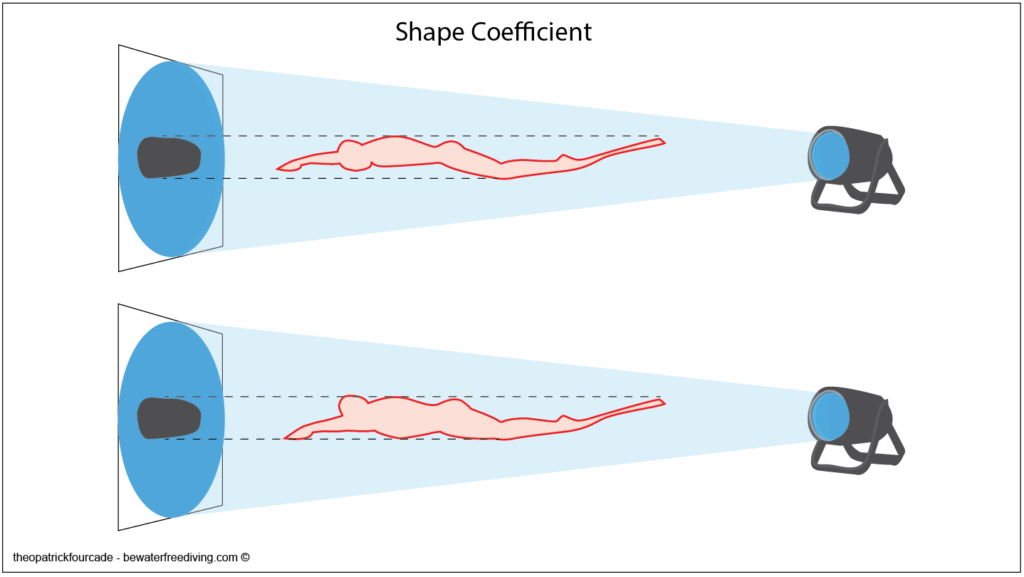
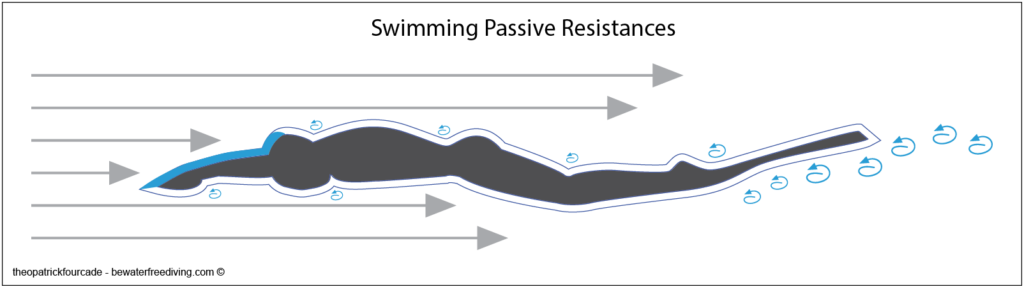
As this shape moves through the water, it will generate certain resistances. All these resistances are called ‘Passive Resistance’. It is the sum of three resistances identified by Counsilman (1968):

Passive Resistance

• Frontal resistance
• Friction resistance
• Drag resistance

These resistances are known as passive, and are the result of the action of the water on the swimmer’s body, which the swimmer undergoes passively.

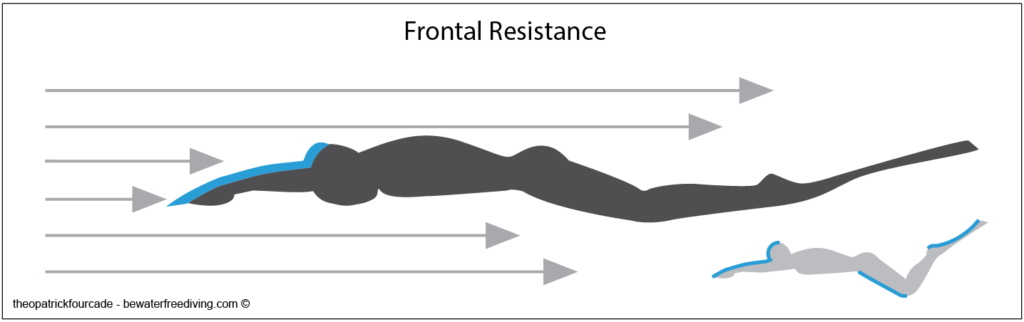
Frontal resistance
This is the resistance created by the surface of the body facing forward. This surface is called the master torque, and it will create resistance when entering the water.

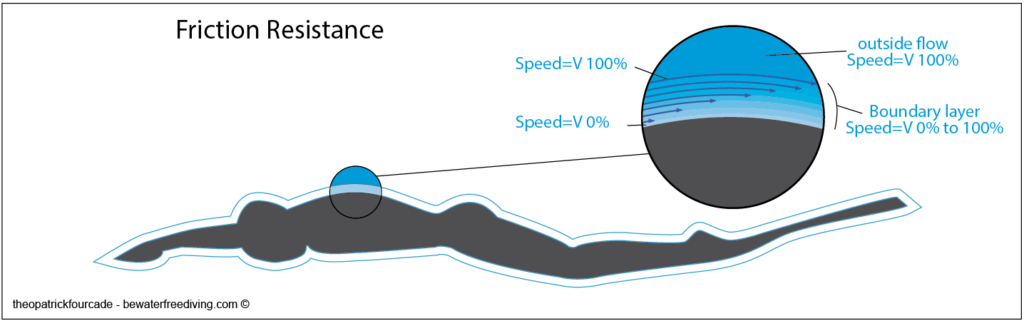
Friction resistance
As the swimmer moves through the water, the water molecules closest to the body (skin or wetsuit) adhere to it. The speed of these molecules is therefore zero. As you move away from the body, the speed of these water molecules increases until it reaches the speed of the other water molecules in the ‘outer flow’. The thin layer of water in which the velocity increases is called the ‘boundary layer’ (Jacques Lachnitt 1978). The fact that two infinitely adjacent layers of water have different velocities results in significant viscosity forces. This is known as frictional resistance.

Drag resistance
This is a vortex resistance also known as tail suction. This resistance to forward motion is extremely detrimental: it causes a suction effect at the rear of the body.

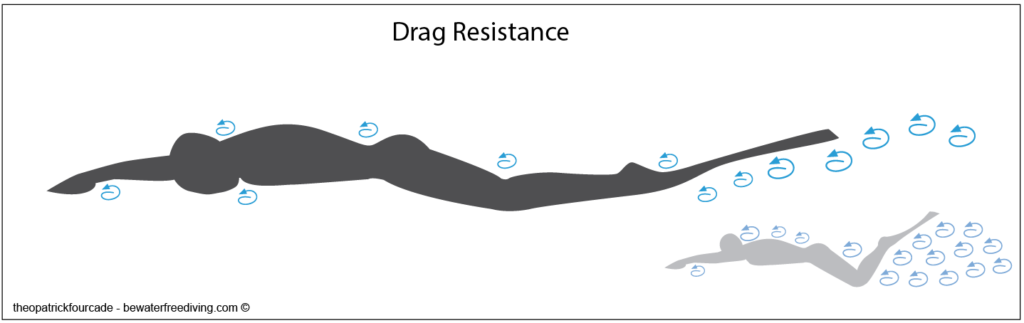
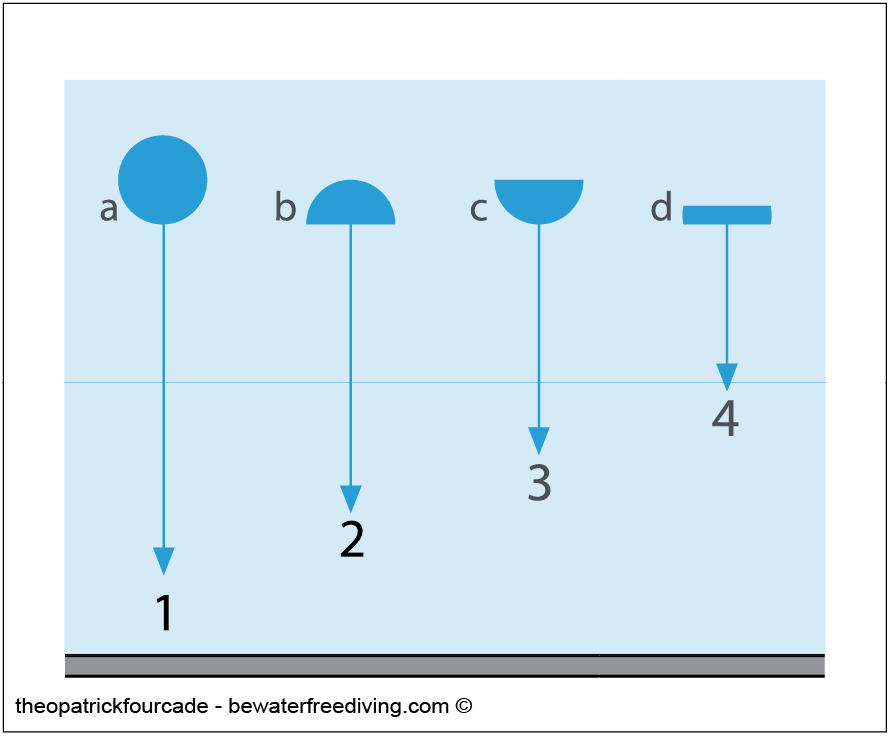
NB: Between the frontal resistance and the drag resistance, which of these two resistances is the most penalising?
The results of the following experiment provide an interesting answer. When 4 objects (a, b, c, d) of the same weight and the same surface area are dropped into the water (assuming they maintain their trajectory as they fall), their order of arrival on the ground will depend on the size of their frontal resistance and their drag resistance.
– The sphere ‘a’ arrives first: it has less frontal and drag resistance than the other three objects.
– The disc ‘d’ comes last: it has more drag and frontal resistance than the other three objects.
– Half-sphere ‘b’ comes before half-sphere ‘c’.
Conclusion: drag resistance is more penalising than frontal resistance.

NB : Wave resistance
Wave resistance is linked to movements close to the surface of the water. As the swimmer moves, they create a zone of turbulence that produces waves: the front wave at the front of the body and the tail wave at the back. These two waves slow down the swimmer’s progress because they form high-pressure zones. To minimise this resistance, the finned swimmer uses the position of his hands to create an additional wave at the front of the body, which interferes with the bow wave to give rise to a reduced resultant wave, known as the Bulb effect. At the bow of some boats there is a cylindrical bulge called a bulb. Its function is to create an additional wave at the bow, the trough of which falls where the bow wave should be. The two waves interfere negatively and tend to cancel each other out, which considerably reduces resistance. During a Dynamic event, a freediver may be confronted with this resistance if he gets too close to the surface. To avoid this resistance completely, he must remain at a depth greater than 3 times his body diameter throughout the event.

Summary of passive resistances

Aquatic propulsion

If we try to reduce passive resistances, we will also try to create active resistances that will act as propulsive supports: these are known as propulsive resistances. It is by creating and maintaining propulsive resistances that we move through the water.

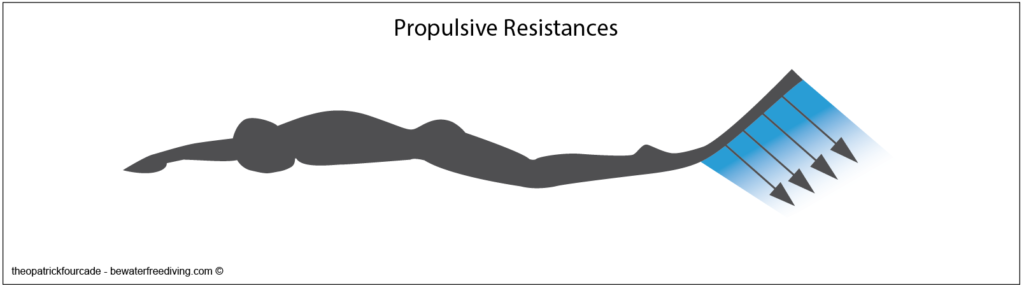
The term ‘propulsive drag resistance’ is used for all resistances resulting from or contributing to propulsive drag.

Synthèse de toutes les résistances passives et actives

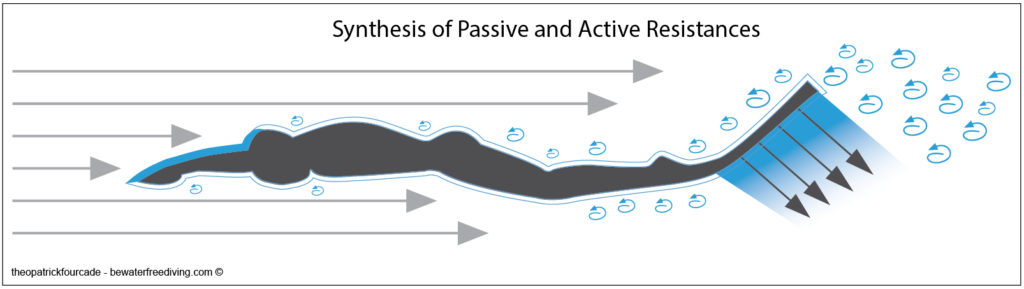
Monofin swimming is the fastest of all strokes, the ‘Formula 1’ of fins sports. The swimming technique that has evolved over the last 50 years is the one that best adapts to the reduction in resistance to forward movement. It is the one that produces the propulsive movement with the lowest ratio of propulsive drag resistance.

Hydrodynamic law applicable to the monofin

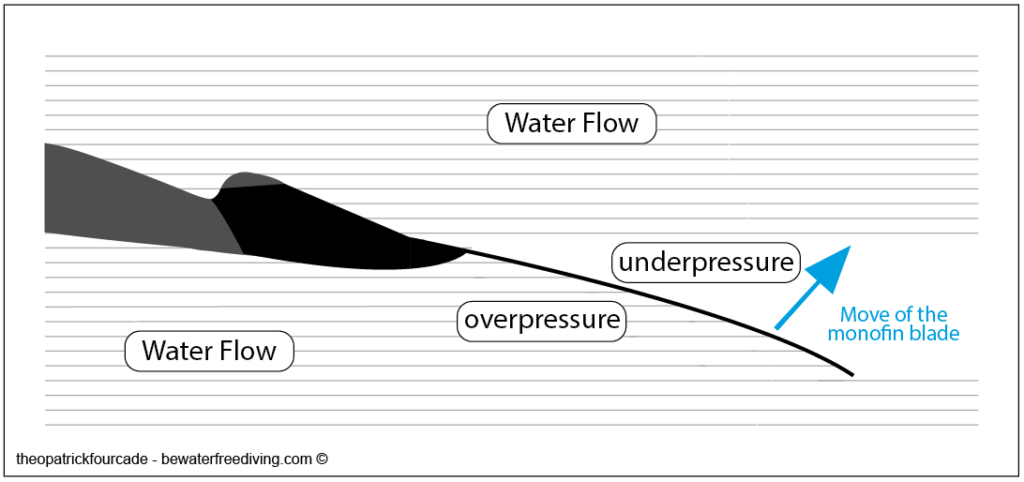
Is the monofin like an aeroplane wing?
At least theoretically, we can consider that the monofin, under the effect of the flow of water (laminar flow) which passes under and over the monofin, creating a zone of high pressure (overpressure) and a zone of low pressure (depression), is helped in its horizontal replacement. The areas of overpressure repel, those of underpressure attract.

Résistance et Vitesse : R=KSV²

It is interesting to understand the equation R=KSV², which summarises the mechanical components of resistance to forward motion (R = Resistance, K = Coefficient corresponding to the shape of the body, S = Surface area of the master torque, V= Speed).

(NB: R=KSV² is true for a rigid body. However, swimmers have a variable geometry and try to minimise resistance. Physiological measurements show that for a swimmer the exponent is less than 2. Di Prampero gives an exponent of 1.2, which seems to be suitable for an immersion swimmer. For surface swimming, an exponent of 1.5 would be more realistic).

In this corrected equation, R=KSV^1.2, the velocity increased by an exponent shows that it is a determining component.
If speed is zero, then resistance to forward motion is zero. However, when moving, the speed factor has an essential effect on resistance to forward movement.
If the speed is 1 m per second, we have : R=KxSx1
If the speed is 2m per second we have : R=KxSx2,3
In apnea, we often speak of speeds of around 1m per second. Resistance to forward movement is therefore not increased by the speed component, but the fact remains that if your swimming style is not hydrodynamic (K and S are not optimised), then throughout your performance you will produce a greater effort than necessary to move forward.

For example, a finswimmer can reach 3.6m per second (R=KxSx4.65). Swimming fast means really coming to terms with different types of resistance. A good time implies an ability to reduce resistance to progress. Each time you improve your time, you will have objectively improved your style.

Swimming with a monofin for a freediver with an effective style is not an impossible task. Most of the technical faults that I observe in freedivers are mainly the result of poor or non-learning of the technique of swimming with a monofin. The result is significant passive and active resistance which, if reduced, would make it easier to perform, especially at the end of an effort: less fatigue, less oxygen consumption, less CO2 production, less lactate accumulation, more serenity, more lucidity, more efficiency, less risk of losing motor control, less risk of syncope.

So you need to optimise your style by working on your technique. To overcome resistance to progress, remember to include regular (timed) speed sessions in your pool training (using a front snorkel, for example, or working on the 100m speed apnea). It’s essential!

References :
Approche Scientifique de la Natation Sportive, 1992 Didier Chollet
La mécanique des fluides, 1978 Jacques Lachnitt
The Science of Swimming, 1968 James E. Cousilman
The Energy Cost of Human Locomotion on Land and in Water, 1986 Di Prampero (equation N°17)